Bridging Traditional and Machine Learning-based Algorithms for Solving PDEs: The Random Feature Method
Jingrun Chen, Xurong Chi, Weinan E, Zhouwang yang
原文链接:https://doi.org/10.4208/jml.220726
实验室科学计算方向2021级博士研究生池煦荣同学的工作《Bridging Traditional and Machine Learning-based Algorithms for Solving PDEs: The Random Feature Method》发表于由鄂维南院士担任主编的期刊Journal of Machine Learning。该研究聚焦于攻克传统数值方法在应对复杂几何问题时的固有局限,以及机器学习方法求解偏微分方程(PDEs)时存在的数值精度偏低且难以系统性提升等关键难题,创新性地提出了一种融合传统数值方法与机器学习方法优势的新型微分方程数值方法。
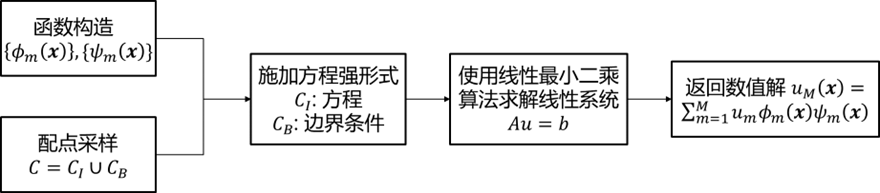
图1.随机特征方法流程图
本研究提出了随机特征方法(Random Feature Method, RFM),融合传统数值方法与机器学习优势,旨在实现高精度、无网格的 PDEs 求解。方法核心包括:
1. 随机特征函数表示
l 采用类两层神经网络架构的随机特征函数线性组合逼近解,避免神经网络训练的非凸性问题。
l 通过单位分解(PoU)构建局部随机特征模型,结合全局基函数实现多尺度表示,有效捕捉解的局部细节与整体性质。
2. 配点法与损失函数
l 基于强形式在配点上构建损失函数,一致地处理方程与边界条件,基函数无需满足边界条件,从而提升了对复杂几何的适应性。
l 引入自适应权重缩放策略,平衡损失函数中方程项与边界条件项的贡献,通过线性系统行最大值归一化实现自动参数调优,尤其适用于物理常数差异大的场景。
3. 优化与无网格特性
l 采用最小二乘优化求解线性系统,基于配点法框架避免网格划分,简化复杂几何下的前处理流程。
通过数值实验验证,RFM 在一维至二维问题中实现谱精度收敛,尤其在复杂几何(如多孔介质)和多尺度问题中表现优于传统有限元法(FEM)、物理信息神经网络(PINN)和局部极限学习机(locELM),兼具效率与鲁棒性。
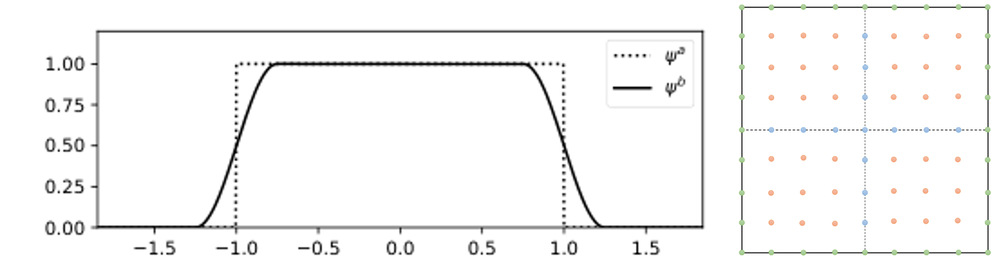
图2. 一维PoU函数与二维区域配点采样示意图
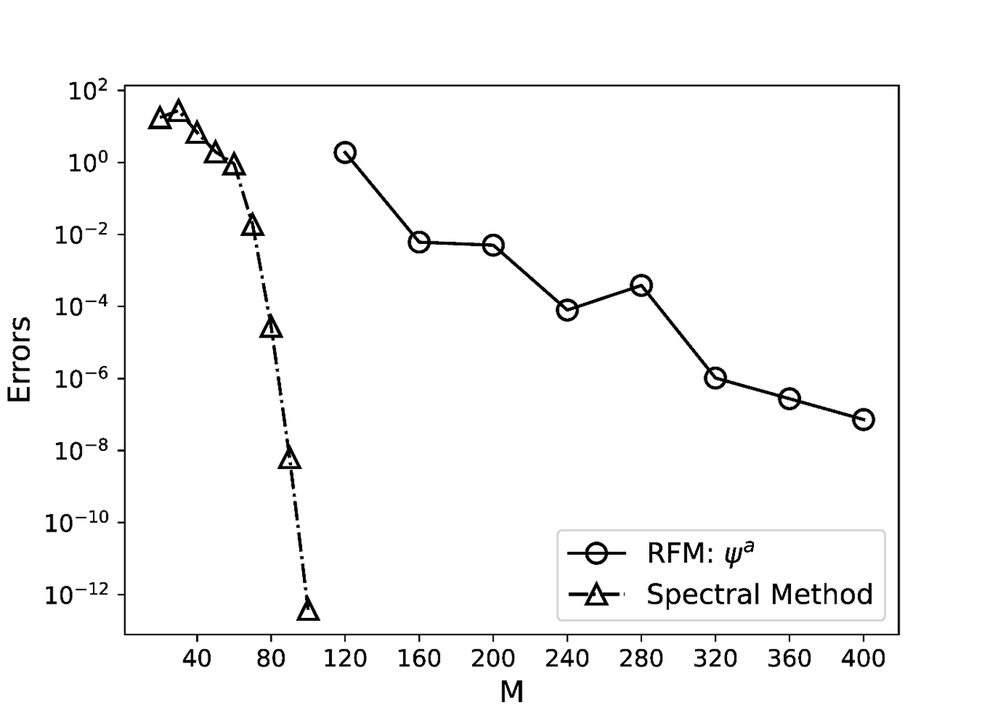
图3. 一维Helmholtz方程半对数数值误差图(RFM具有谱精度)

图4. 二维复杂几何域上的弹性力学问题数值求解
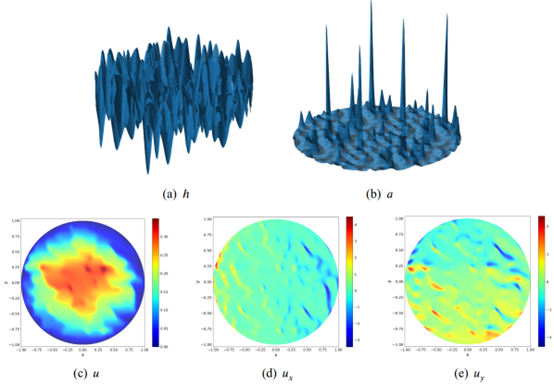
图5. 真解具有多尺度特征的均匀化问题数值求解
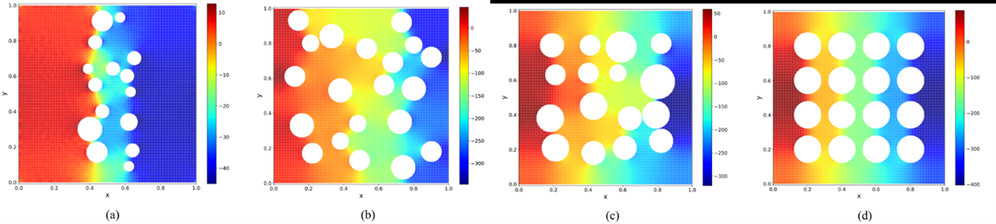
图6. 二维复杂几何域上的Stokes流问题压力