Consensus based Stochastic Optimal Control

Liyao Lyu, Jingrun Chen

原文链接：https://arxiv.org/abs/2501.17801

开源代码：https://github.com/Lyuliyao/Adam_CBO_Control

实验室的最新工作《基于共识的随机最优控制方法》（Consensus  Based Stochastic Optimal Control）发表在ICML 2025。该研究提出了一种无梯度（Gradient-Free）的深度强化学习算法，用于解决高维、有限时间随机控制问题。现有的深度强化学习方法在解决此类问题时，通常通过蒙特卡洛采样直接估计策略梯度，但这种方法往往存在高方差问题。

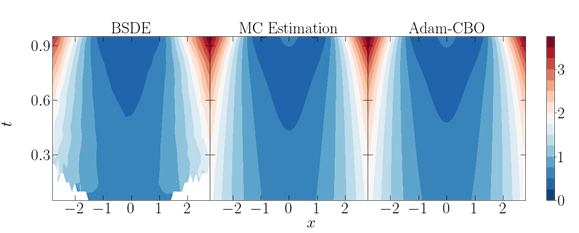
图1. 结果对比图

本研究创新性地引入了动量共识优化框架（Momentum Consensus-Based Optimization, M-CBO）和自适应动量共识优化框架（Adaptive Momentum Consensus-Based Optimization, Adam-CBO）。这些方法通过蒙特卡洛估计值函数而非其梯度来优化策略，利用可调整的高斯噪声支持高效探索，帮助算法在复杂非凸环境中收敛到最优策略。实验结果表明，该方法在不同问题维度下均表现出较高的准确性和可扩展性，并具备扩展到平均场控制问题的潜力。

传统的随机最优控制（SOC）方法，如有限体积法、伽辽金法和单调逼近法，旨在求解相应的Hamilton-Jacobi-Bellman（HJB）方程。然而，这些方法在高维空间中难以扩展，因为计算复杂度会随着状态和动作变量的维度呈指数增长。本研究提出的方法完全基于模型，无需显式建模转移核，同时避免了策略梯度的高方差问题，也不需要离散化状态和动作空间。这些特性使得该方法在高维环境中能够高效扩展，特别适用于时间依赖的最优控制问题。

理论分析表明，在一定的假设条件下，M-CBO方法能够收敛到最优策略。数值实验验证了该方法在多种问题设置下的优越性能，包括线性二次控制问题、Ginzburg-Landau模型和系统性风险平均场控制问题。未来，该方法有望进一步应用于平均场博弈问题和具有部分信息或约束的控制问题。