Two-level random feature methods for elliptic partial differential equations over complex domains

Yifei Sun, Jingrun Chen

原文链接：https://doi.org/10.1016/j.cma.2025.117961

实验室科学计算方向2021级博士研究生孙羿斐同学的最新工作《Two-level random feature methods for elliptic partial differential equations over complex domains》发表在国际计算力学领域顶级期刊《Computer Methods in Applied Mechanics and Engineering》，该工作致力于提升机器学习方法在复杂几何上偏微分方程求解中的效率与准确性。传统的有限元方法在求解区域复杂的偏微分方程时往往依赖人工构建的网格，计算代价与人工成本高。

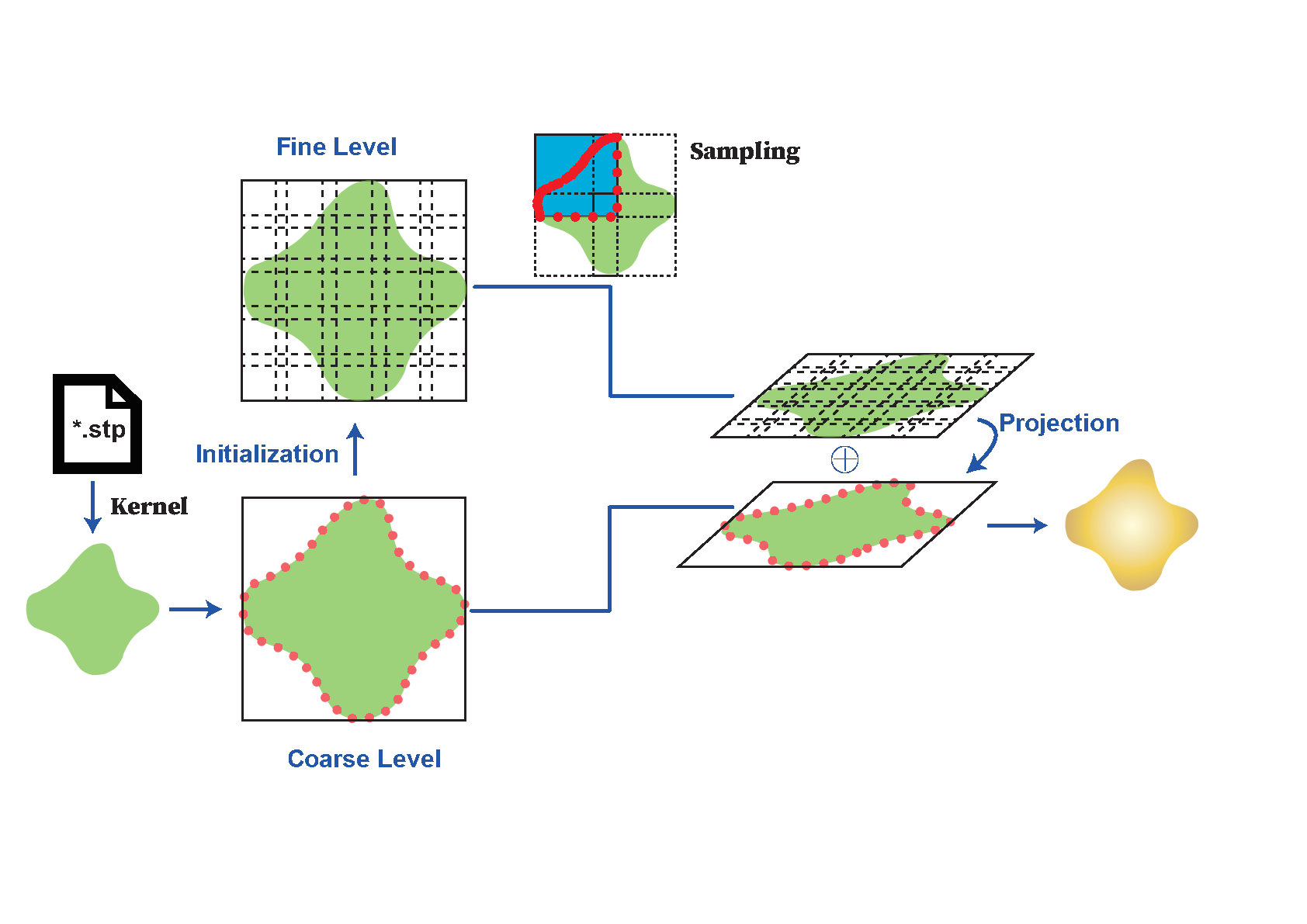
图1. 模型架构图

   本研究基于机器学习中的随机特征方法（Random Feature Method, RFM），结合区域分解思想，提出了“两层随机特征方法”（Two-level RFM），有效缓解了在复杂几何域中求解大规模最小二乘系统的计算压力。具体而言，研究将复杂域划分为多个子区域，在局部子域内利用局部随机特征函数进行逼近，并在全局层面进行统一校正，从而大幅降低计算复杂度。在保持高精度的同时，该方法显著提升了计算效率，具备极强的可扩展性，能够在并行环境下快速收敛。实验结果显示，该方法在求解三维多频率泊松方程、多尺度问题以及结构力学中的典型工程几何时，均表现出优越的精度与稳定性，尤其在传统有限元方法难以网格化或计算效率较低的场景中展现出明显优势。

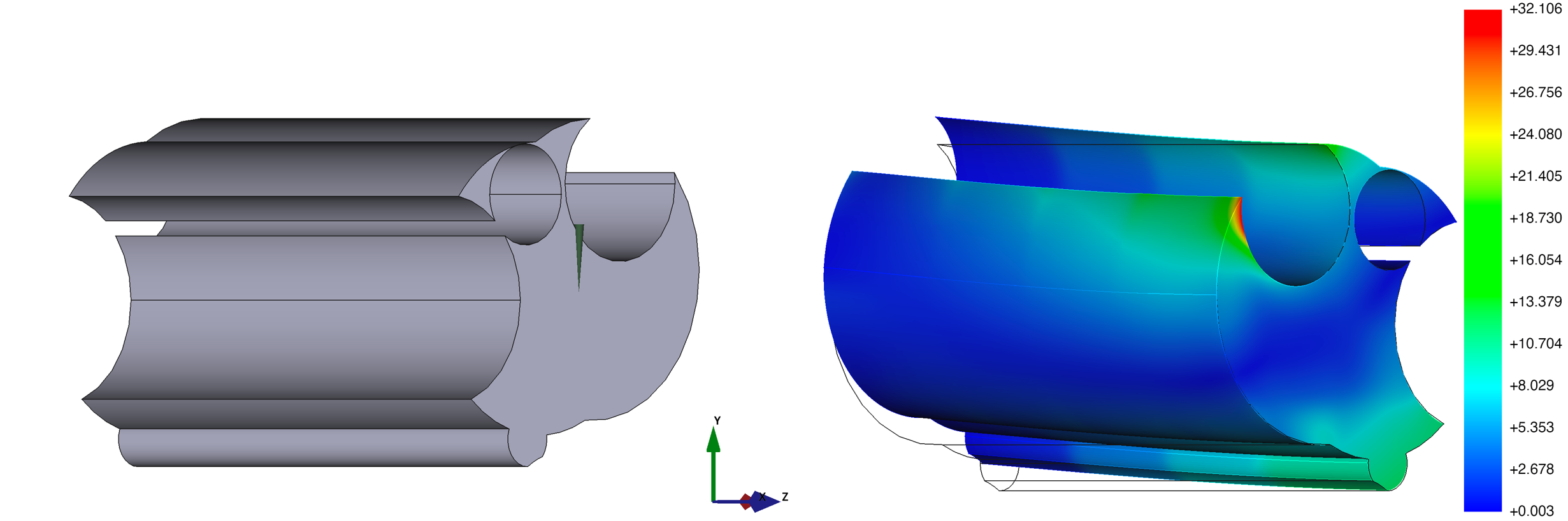
图2. 网格化困难的几何中的结构力学条件设置(左)与应力结果(右)